My ME/CFS improves during summer, in the period of the year that goes from May/June to the end of September (when I am in Rome, Italy). I don’t know why. In a previous study (Maccallini P. 2022), I analyzed the correlation between my symptoms and several environmental parameters, during three periods covering a total of 190 days: in one, I improved while the season was going toward summer, in another one we were in full-blown summer, and in the third one my functioning declined while summer was fading away. The statistical analysis showed a positive correlation between my functionality score and the temperature of the air and a negative correlation between the score and air density and dry air density (remember that the higher the functionality score, the better I feel). No correlation was found between my functionality score and: relative humidity, absolute humidity, atmospheric pressure, and the concentration of particulate with a diameter below or equal to  . In another study, I simulated summerish conditions in a room for five months, during cold months, by means of a heat pump, an infrared lamp, an air moisturizer, and mylar panels (Maccallini P. 2022) and despite an improvement during the experiment, the correlation between my status and air temperature tended to be negative. In the present study, I consider again environmental parameters from a few locations in the temperate and subtropical regions of both hemispheres and I search for the best regression model between them and my status.
. In another study, I simulated summerish conditions in a room for five months, during cold months, by means of a heat pump, an infrared lamp, an air moisturizer, and mylar panels (Maccallini P. 2022) and despite an improvement during the experiment, the correlation between my status and air temperature tended to be negative. In the present study, I consider again environmental parameters from a few locations in the temperate and subtropical regions of both hemispheres and I search for the best regression model between them and my status.
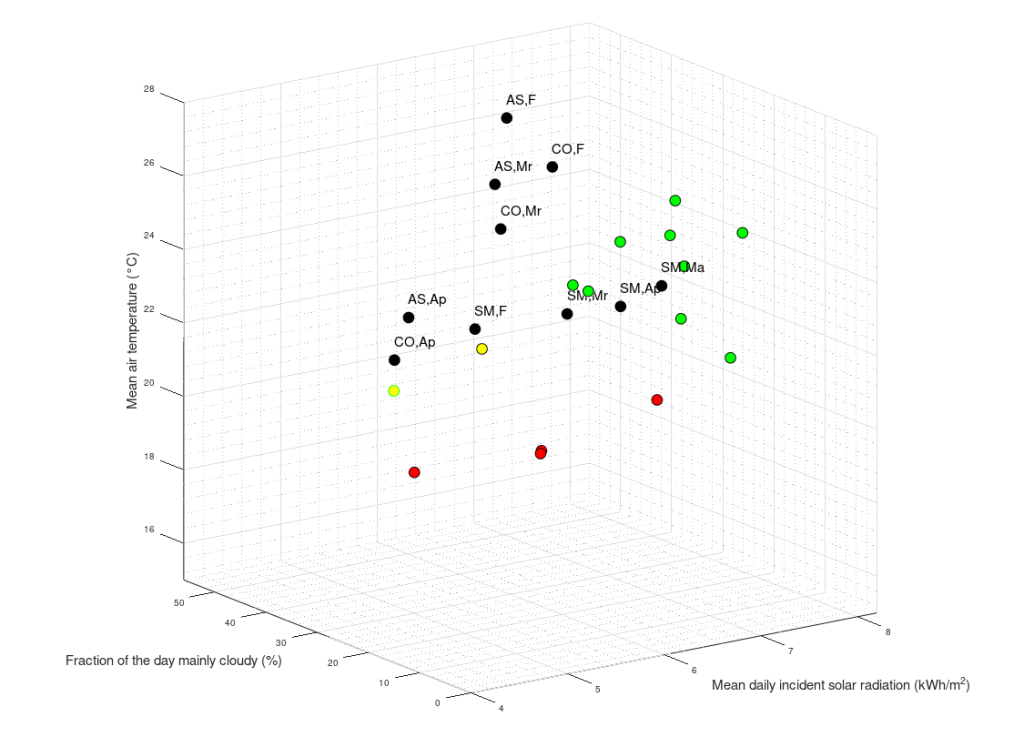
I have considered a set of 20 points defined by the two coordinates City and Month. To each of them, I have assigned a score, from 4 to 6, based on the degree of severity (the lower the score, the worse the disease) of my symptoms in that particular city, for that specific month. For each point City-Month I have collected the monthly mean air temperature (T), mean cloudiness (Cl), and mean solar radiation (R) (Figure 1). I have considered several models of regression between the score (response variable) and the three explanatory variables T, Cl, and R (Table 1). For each regression model, I have calculated the p values of the estimates of the coefficients, and I have also calculated the p value of the F test, given by
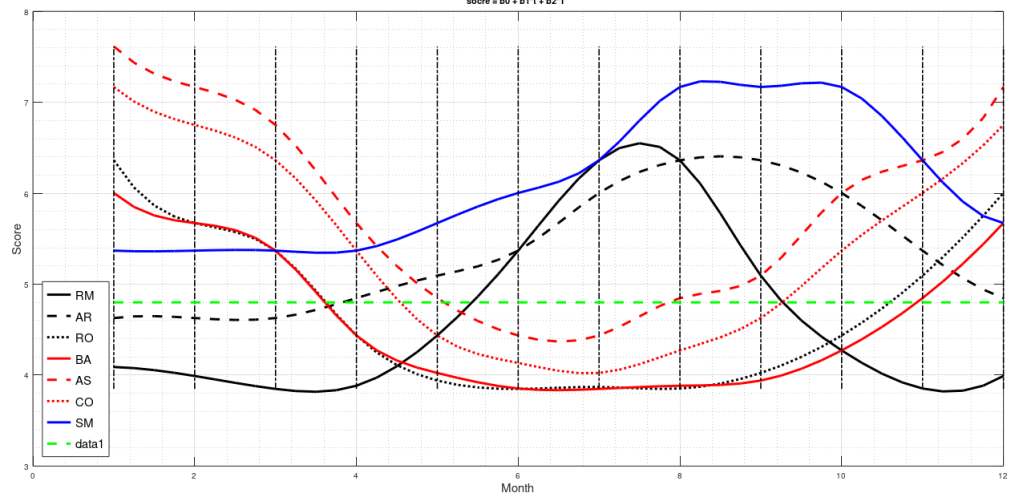
I have used then the best regression model to predict the score along the year in several cities in the temperate and subtropical regions of both hemispheres (Figure 2). The diagrams have been interpolated by using cubic splines, to make them more smooth. These predictions can be used to find the best spot to live in, as a function of the month of the year.
where R is the power exchange in the form of radiant energy, C is the exchange by conduction, CV is the exchange by convection, and E is the dispersion of power by evaporation. This is a simplification of complex phenomena that should also take into account the exchange of thermic power associated with the passage of atmospheric gas through the respiratory system. The power R can be further specified in the form 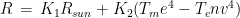 where
where 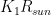 is the power absorbed from the Sun, and the other addend is the radiant power exchanged with the environment, whit
is the power absorbed from the Sun, and the other addend is the radiant power exchanged with the environment, whit 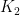 a constant that expresses radiant and geometrical properties of both my body and of the environment. While
a constant that expresses radiant and geometrical properties of both my body and of the environment. While 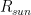 is radiant power in the form of short wave radiation (wavelength below 3
is radiant power in the form of short wave radiation (wavelength below 3 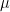 ), the other addend represents radiant power exchanged by bodies at low temperatures with a wavelength above 3
), the other addend represents radiant power exchanged by bodies at low temperatures with a wavelength above 3 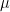 (according to the Stephan-Boltzman law) (R). But what temperature is
(according to the Stephan-Boltzman law) (R). But what temperature is  ? One first approximation might be the absolute temperature of the air, because in warm months, with the windows open, the objects surrounding us tend to acquire a superficial temperature similar to that of the air. To show that point, I analyzed the power emitted by the soil in Rome, during the year 2020, and the temperature of the air (data from ARPALAZIO). If we indicate J the daily mean power emitted per surface unit by the soil in the hemispace, the Stefan-Boltzmann law states that
? One first approximation might be the absolute temperature of the air, because in warm months, with the windows open, the objects surrounding us tend to acquire a superficial temperature similar to that of the air. To show that point, I analyzed the power emitted by the soil in Rome, during the year 2020, and the temperature of the air (data from ARPALAZIO). If we indicate J the daily mean power emitted per surface unit by the soil in the hemispace, the Stefan-Boltzmann law states that
And this is in fact the case, we have the regression in Figure 3, with a p value of the F test below  . For further details on these calculations, see (Maccallini P, 2022).
. For further details on these calculations, see (Maccallini P, 2022).
As for the exchange of power by conduction and convection, in both cases, they are expressed by a constant multiplied by the difference in temperature between my skin and the air. That said, we can write again eq. 1 as follows:
were we have removed the term linked to evaporation. In other words, the power exchanged by my body with the environment could be expressed, in first approximation, by the equation
This is model 5 of Table 1. If we consider the case of a subject who rarely leaves home, we can get rid of 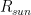 and we get model 7, the best model of regression. In a previous article, I showed that the best correlation between my status and several environmental parameters was with air temperature (R), and yet in an experiment where I simulated summer in a room with the use of a heat pump, an infrared lamp, and an air moisturizer, there was no correlation between my status and air temperature (R) (in fact the correlation had a tendency to be negative). From the perspective of this new study, I would explain the previous results as follows: in the first study performed during worm months using environmental parameters we caught the Spearman’s correlation between my status and air temperature which was a reflection of the correlation between my status and the longwave infrared radiation from the environment (proportional to the fourth power of the absolute temperature of the air); in the second study, performed during cold months within a room with artificially heated air, there was no correlation between air temperature and the infrared emission of the environment (which came from a lamp), so we found a correlation that tended to be negative perhaps because when I was feeling worse I raised the temperature of the air. It should be noted though that in models 7 and 5 the coefficient of t is negative, therefore it seems that while the longwave infrared radiation plays a positive role, the temperature of the air does not.
and we get model 7, the best model of regression. In a previous article, I showed that the best correlation between my status and several environmental parameters was with air temperature (R), and yet in an experiment where I simulated summer in a room with the use of a heat pump, an infrared lamp, and an air moisturizer, there was no correlation between my status and air temperature (R) (in fact the correlation had a tendency to be negative). From the perspective of this new study, I would explain the previous results as follows: in the first study performed during worm months using environmental parameters we caught the Spearman’s correlation between my status and air temperature which was a reflection of the correlation between my status and the longwave infrared radiation from the environment (proportional to the fourth power of the absolute temperature of the air); in the second study, performed during cold months within a room with artificially heated air, there was no correlation between air temperature and the infrared emission of the environment (which came from a lamp), so we found a correlation that tended to be negative perhaps because when I was feeling worse I raised the temperature of the air. It should be noted though that in models 7 and 5 the coefficient of t is negative, therefore it seems that while the longwave infrared radiation plays a positive role, the temperature of the air does not.
The three best regression models suggest that my improvement is linked to the thermal energy balance of the body: the lower the dispersion of radiant thermic energy, the better I feel. But at the same time, the temperature of the air has a detrimental effect. But other interpretations might be possible: there might be an effect of thermal radiation on my biology that is not linked to thermic homeostasis but instead to some other biological targets. Moreover, there might be other models of regression that I have not considered, that perform better than the ones mentioned.
The first script is written in Octave. It calculates the regressions and their F tests (by using a custom subroutine) and it plots Figure 1 and Figure 2. It also writes the data in csv format for the second script (in R), which performs the same statistical analyses and also calculates the p values associated with each coefficient estimate.
% file name = Spot_finder_2
% date of creation = 29/01/2023
%
close all
clear all
#
pkg load statistics % we need this package for the F law
spline = 1 % it is one if we want a cubic spline interpolation for the last plot
#
#-------------------------------------------------------------------------------
# Data
#-------------------------------------------------------------------------------
#
months = ["Je"; "F"; "Mr"; "Ap"; "Ma"; "Jn"; "Jl"; "Au"; "S"; "O"; "N"; "D"];
%
% data of Rome (RM), Italy
%
k=1;
Spot(1,:,k) = [2,3,4.3,5.6,6.8,7.5,7.5,6.5,4.9,3.4,2.2,1.8]; % Mean daily incident solar radiation (kWh/m^2)
Spot(2,:,k) = [47,44,44,43,39,25,13,18,32,43,47,46]; % Fraction of the day mainly cloudy (%)
Spot(3,:,k) = [7,8,11,13,18,22,25,25,21,17,12,8]; % Mean air temperature (°C)
Spot(4,:,k) = [3,3,6,8,12,16,18,18,15,12,7,4]; % Min air temperature (°C)
Spot(5,:,k) = [12,13,16,19,23,27,31,31,27,22,17,13]; % Max air temperature (°C)
%
% data of Arona (AR), Tenerife, Spain
%
k=2;
Spot(1,:,k) = [3.9,4.9,6.1,7.2,7.8,8.2,8.0,7.4,6.3,5.1,4.0,3.5]; % Mean daily incident solar radiation (kWh/m^2)
Spot(2,:,k) = [32,28,26,24,21,9,2,6,21,34,38,36]; % Fraction of the day mainly cloudy (%)
Spot(3,:,k) = [19,19,19,20,21,22,24,25,25,24,22,20]; % Mean air temperature (°C)
Spot(4,:,k) = [16,16,16,17,18,20,21,22,22,21,19,17]; % Min air temperature (°C)
Spot(5,:,k) = [22,22,23,23,24,26,28,28,28,27,25,23]; % Max air temperature (°C)
%
% data of Rosario (RO), Santa Fe, Argentina
%
k=3;
Spot(1,:,k) = [7.6,6.7,5.6,4.3,3.2,2.7,3.0,3.9,5.1,6.3,7.3,7.7]; % Mean daily incident solar radiation (kWh/m^2)
Spot(2,:,k) = [28,28,28,34,45,47,44,40,36,32,30,28]; % Fraction of the day mainly cloudy (%)
Spot(3,:,k) = [25,23,22,18,14,11,10,12,15,18,21,24]; % Mean air temperature (°C)
Spot(4,:,k) = [19,18,17,13,10,7,6,7,9,13,16,18]; % Min air temperature (°C)
Spot(5,:,k) = [30,29,27,23,19,16,16,18,21,24,27,29]; % Max air temperature (°C)
%
% data of Buenos Aires (BA), Argentina
%
k=4;
Spot(1,:,k) = [7.6,6.7,5.5,4.1,3.0,2.5,2.7,3.6,4.8,6.2,7.3,7.8]; % Mean daily incident solar radiation (kWh/m^2)
Spot(2,:,k) = [29,31,31,38,48,50,48,45,41,37,33,30]; % Fraction of the day mainly cloudy (%)
Spot(3,:,k) = [24,23,22,18,15,12,11,13,14,17,20,23]; % Mean air temperature (°C)
Spot(4,:,k) = [21,20,19,15,12,9,9,10,11,14,17,19]; % Min air temperature (°C)
Spot(5,:,k) = [28,27,25,21,18,15,14,16,18,21,24,27]; % Max air temperature (°C)
%
% data of Asuncion (AS), Paraguay
%
k=5;
Spot(1,:,k) = [7.0,6.6,6.0,5.0,4.1,3.5,3.8,4.5,5.3,6.1,6.9,7.1]; % Mean daily incident solar radiation (kWh/m^2)
Spot(2,:,k) = [45,42,33,31,32,37,35,32,32,38,38,42]; % Fraction of the day mainly cloudy (%)
Spot(3,:,k) = [28,27,26,23,20,18,18,20,21,24,25,27]; % Mean air temperature (°C)
Spot(4,:,k) = [23,23,21,19,16,14,14,15,16,19,21,22]; % Min air temperature (°C)
Spot(5,:,k) = [33,32,31,28,25,23,23,25,27,29,31,32]; % Max air temperature (°C)
%
% data of Corrientes (CO), Argentina
%
k=6;
Spot(1,:,k) = [7.2,6.7,5.9,4.8,3.9,3.4,3.6,4.3,5.3,6.2,7.0,7.3]; % Mean daily incident solar radiation (kWh/m^2)
Spot(2,:,k) = [39,35,30,30,33,37,35,33,32,34,34,36,]; % Fraction of the day mainly cloudy (%)
Spot(3,:,k) = [27,26,25,22,18,16,15,17,19,22,24,26]; % Mean air temperature (°C)
Spot(4,:,k) = [22,22,20,17,14,12,11,12,14,17,19,21]; % Min air temperature (°C)
Spot(5,:,k) = [33,32,30,26,23,21,21,23,25,27,29,31]; % Max air temperature (°C)
%
% data of SantaMaria (SM), Capo Verde
%
k=7;
Spot(1,:,k) = [5.0,5.9,6.8,7.3,7.3,7.2,6.7,6.2,5.8,5.6,5.0,4.6]; % Mean daily incident solar radiation (kWh/m^2)
Spot(2,:,k) = [42,35,34,33,25,19,36,53,56,48,54,49]; % Fraction of the day mainly cloudy (%)
Spot(3,:,k) = [22,22,22,22,23,24,25,27,27,27,25,23]; % Mean air temperature (°C)
Spot(4,:,k) = [20,19,20,20,21,22,23,25,25,24,23,21]; % Min air temperature (°C)
Spot(5,:,k) = [25,25,25,26,26,27,28,30,30,30,28,26]; % Max air temperature (°C)
%
names = {"RM","AR","RO","BA","AS","CO","SM"};
types = {"-k","--k",":k","-r","--r",":r","-b","--b","-.b",}
%
for i=1:5
max_measure(i) = max([Spot(i,:,1),Spot(i,:,2),Spot(i,:,3),Spot(i,:,4),Spot(i,:,5),Spot(i,:,6),Spot(i,:,7)])
endfor
%
%-------------------------------------------------------------------------------
% Subroutine for F-test
%-------------------------------------------------------------------------------
%
function [pval,R2,TS] = F_test (M,b,beta)
r = length(M(1,:))-1; % number of explanatory variables
n = length(M(:,1)) % number of data points
R = b-M*beta; % residues
SSR = 0;
Sbb = 0;
for i=1:n
SSR = SSR + R(i)^2; % sum of squared residues
Sbb = Sbb + b(i)^2;
endfor
Sbb = Sbb - n*(mean(b))^2;
R2 = (Sbb - SSR)/Sbb; % R squared
TS = R2*(n-r-1)/(r*(1-R2)); % test statistics
pval = 1 - fcdf(TS,r,n-r-1); % F-test
endfunction
%
%-------------------------------------------------------------------------------
% Subroutine plot_score
%-------------------------------------------------------------------------------
%
function Plot_score (score, h, model, names, types, spline)
figure(5) % Plotting of the Scoring for the query spots
%
for k=1:length(names)
if (spline==1)
yi = interp1([1:1:12],score(:,k),[1:0.25:12],"spline")
plot([1:0.25:12],yi,char(types{k}),"linewidth",1.5)
hold on
else
plot([1:1:12],score(:,k),char(types{k}),"linewidth",1.5)
hold on
endif
endfor
plot([1,12],[5,5],"--g","linewidth",1.5)
title(model{h})
legend(char(names{1:length(names)}),"location","southwest",'fontsize',15)
xlabel("Month",'fontsize',15);
ylabel("Score",'fontsize',15);
grid on
grid minor on
endfunction
%
%-------------------------------------------------------------------------------
figure 1 % mean temp, irradiation, cloudiness with storing of data for regressions
%-------------------------------------------------------------------------------
%
% plotting Rome
%
k=1;
n=1;
for i=1:12
if (and(i>=6,i<9))
plot3(Spot(1,i,k),Spot(2,i,k),Spot(3,i,k),'o','markersize',6,'markerfacecolor','g','markeredgecolor','k')
b(n)=6;
M(n,1:4)=[1,Spot(1,i,k),Spot(2,i,k),Spot(3,i,k)];
n=n+1
endif
if (or(i<6,i>9))
plot3(Spot(1,i,k),Spot(2,i,k),Spot(3,i,k),'o','markersize',6,'markerfacecolor','r','markeredgecolor','k')
endif
if (or(and(i>3,i<5),i>9))
b(n)=4;
M(n,1:4)=[1,Spot(1,i,k),Spot(2,i,k),Spot(3,i,k)];
n=n+1
endif
if (i==5)
b(n)=5;
M(n,1:4)=[1,Spot(1,i,k),Spot(2,i,k),Spot(3,i,k)];
n=n+1
endif
if (i==9)
plot3(Spot(1,i,k),Spot(2,i,k),Spot(3,i,k),'o','markersize',6,'markerfacecolor','y','markeredgecolor','g')
b(n)=5.7;
M(n,1:4)=[1,Spot(1,i,k),Spot(2,i,k),Spot(3,i,k)];
n=n+1
endif
hold on
endfor
%
% plotting Arona
%
k=2;
for i=1:12
if (i==5)
plot3(Spot(1,i,k),Spot(2,i,k),Spot(3,i,k),'o','markersize',6,'markerfacecolor','g','markeredgecolor','k')
b(n)=6
M(n,1:4)=[1,Spot(1,i,k),Spot(2,i,k),Spot(3,i,k)];
n=n+1
endif
if (and(i>=1,i<5))
plot3(Spot(1,i,k),Spot(2,i,k),Spot(3,i,k),'o','markersize',6,'markerfacecolor','r','markeredgecolor','k')
b(n)=4
M(n,1:4)=[1,Spot(1,i,k),Spot(2,i,k),Spot(3,i,k)];
n=n+1
endif
hold on
endfor
%
% plotting Rosario
%
k=3;
for i=1:12
if (and(i>=1,i<3))
plot3(Spot(1,i,k),Spot(2,i,k),Spot(3,i,k),'o','markersize',6,'markerfacecolor','g','markeredgecolor','k')
b(n)=6
M(n,1:4)=[1,Spot(1,i,k),Spot(2,i,k),Spot(3,i,k)];
n=n+1
endif
if (i==3)
plot3(Spot(1,i,k),Spot(2,i,k),Spot(3,i,k),'o','markersize',6,'markerfacecolor','y','markeredgecolor','k')
b(n)=5.5
M(n,1:4)=[1,Spot(1,i,k),Spot(2,i,k),Spot(3,i,k)];
n=n+1
endif
hold on
endfor
%
% plotting CABA
%
k=4;
for i=1:12
if (or(i==12,i==1,i==2))
plot3(Spot(1,i,k),Spot(2,i,k),Spot(3,i,k),'o','markersize',6,'markerfacecolor','g','markeredgecolor','k')
b(n)=6
M(n,1:4)=[1,Spot(1,i,k),Spot(2,i,k),Spot(3,i,k)];
n=n+1
endif
if (i<12)
hold on
endif
endfor
%
% plotting query spots
%
% Asuncion
%
k=5;
for i=2:4
plot3(Spot(1,i,k),Spot(2,i,k),Spot(3,i,k),'o','markersize',6,'markerfacecolor','k','markeredgecolor','k')
text(Spot(1,i,k),Spot(2,i,k),Spot(3,i,k)+0.5, strcat(char(names{k}),", ",months(i,:)),'fontsize',15)
endfor
%
% Corrientes
%
k=6;
for i=2:4
plot3(Spot(1,i,k),Spot(2,i,k),Spot(3,i,k),'o','markersize',6,'markerfacecolor','k','markeredgecolor','k')
text(Spot(1,i,k),Spot(2,i,k),Spot(3,i,k)+0.5, strcat(char(names{k}),", ",months(i,:)),'fontsize',15)
endfor
%
% Santa Maria
%
k=7;
for i=2:5
plot3(Spot(1,i,k),Spot(2,i,k),Spot(3,i,k),'o','markersize',6,'markerfacecolor','k','markeredgecolor','k')
text(Spot(1,i,k),Spot(2,i,k),Spot(3,i,k)+0.5, strcat(char(names{k}),", ",months(i,:)),'fontsize',15)
endfor
%
grid on
grid minor on
xlabel("Mean daily incident solar radiation (kWh/m^{2})",'fontsize',15);
ylabel("Fraction of the day mainly cloudy (%)",'fontsize',15);
zlabel("Mean air temperature (°C)",'fontsize',15);
axis ('square')
axis([4,max_measure(1),0,max_measure(2),15,max_measure(3)])
%
%-------------------------------------------------------------------------------
% Regressions
%-------------------------------------------------------------------------------
%
n=n-1; % number of measures
%
b = transpose(b)
x = cell() % it contains the coefficients of the models
model = cell() % it contains the description of the models
matrix = cell() % it contains the matrix of the regression
k = 0;
%
for i=1:n
A(i,1:3)=[1,M(i,2),M(i,4)]
endfor
k = k+1;
[x{k}, std, mse, S] = lscov (A, b)
[pval(k), R2(k), TS(k)] = F_test (A, b, x{k})
model{k} = "socre = b0 + b1*Rad + b2*t"
matrix{k} = A;
clear A
%
for i=1:n
A(i,1:3)=[1,M(i,3),M(i,4)]
endfor
k = k+1;
[x{k}, std, mse, S] = lscov (A, b)
[pval(k), R2(k), TS(k)] = F_test (A, b, x{k})
model{k} = "socre = b0 + b1*Cl + b2*t"
matrix{k} = A;
clear A
%
for i=1:n
A(i,1:4)=[1,M(i,2),M(i,3),M(i,4)]
endfor
k = k+1;
[x{k}, std, mse, S] = lscov (A, b)
[pval(k), R2(k), TS(k)] = F_test (A, b, x{k})
model{k} = "socre = b0 + b1*Rad + b1*Cl + b2*t"
matrix{k} = A;
clear A
%
for i=1:n
A(i,1:3)=[1,M(i,2),(273.15+M(i,4))^4]
endfor
k = k+1;
[x{k}, std, mse, S] = lscov (A, b)
[pval(k), R2(k), TS(k)] = F_test (A, b, x{k})
model{k} = "socre = b0 + b1*Rad + b2*T^{4}"
matrix{k} = A;
clear A
%
for i=1:n
A(i,1:4)=[1,M(i,2),M(i,4),(273.15+M(i,4))^4]
endfor
k = k+1;
[x{k}, std, mse, S] = lscov (A, b)
[pval(k), R2(k), TS(k)] = F_test (A, b, x{k})
model{k} = "socre = b0 + b1*Rad + b2*t + b3*T^{4}"
matrix{k} = A;
clear A
%
for i=1:n
A(i,1:2)=[1,(273.15+M(i,4))^4]
endfor
k = k+1;
[x{k}, std, mse, S] = lscov (A, b)
[pval(k), R2(k), TS(k)] = F_test (A, b, x{k})
model{k} = "socre = b0 + b1*T^{4}"
matrix{k} = A;
clear A
%
for i=1:n
A(i,1:3)=[1,M(i,4),(273.15+M(i,4))^4]
endfor
k = k+1;
[x{k}, std, mse, S] = lscov (A, b)
[pval(k), R2(k), TS(k)] = F_test (A, b, x{k})
model{k} = "socre = b0 + b1*t + b2*T^{4}"
matrix{k} = A;
clear A
%
%-------------------------------------------------------------------------------
% Selection of the best model
%-------------------------------------------------------------------------------
%
for i=1:length(pval)
if (pval(i)==min(pval))
best=i;
endif
endfor
%
%-------------------------------------------------------------------------------
% Region of the plane Rad-Temp with high score according to the regression
% model
%-------------------------------------------------------------------------------
%
R(1)= 4;
R(2)= max_measure(1);
Temp_R(1) = ( 5.5 - x{1}(1) - x{1}(2)*R(1) )/x{1}(3);
Temp_R(2) = ( 5.5 - x{1}(1) - x{1}(2)*R(2) )/x{1}(3);
%
%-------------------------------------------------------------------------------
% Region of the plane Cloudiness-Temp with high score according to the regression
% model
%-------------------------------------------------------------------------------
%
Cl(1)= 0;
Cl(2)= max_measure(2);
Temp_Cl(1) = ( 5.5 - x{2}(1) - x{2}(2)*Cl(1) )/x{2}(3);
Temp_Cl(2) = ( 5.5 - x{2}(1) - x{2}(2)*Cl(2) )/x{2}(3);
%
%-------------------------------------------------------------------------------
figure 2 % mean temp and irradiation
%-------------------------------------------------------------------------------
%
% plotting Rome
%
k=1;
for i=1:12
if (and(i>=6,i<9))
plot(Spot(1,i,k),Spot(3,i,k),'o','markersize',6,'markerfacecolor','g','markeredgecolor','k')
endif
if (or(i<6,i>9))
plot(Spot(1,i,k),Spot(3,i,k),'o','markersize',6,'markerfacecolor','r','markeredgecolor','k')
endif
if (i==9)
plot(Spot(1,i,k),Spot(3,i,k),'o','markersize',6,'markerfacecolor','y','markeredgecolor','g')
endif
hold on
endfor
%
% plotting Arona
%
k=2;
for i=1:12
if (i==5)
plot(Spot(1,i,k),Spot(3,i,k),'o','markersize',6,'markerfacecolor','g','markeredgecolor','k')
endif
if (and(i>=1,i<5))
plot(Spot(1,i,k),Spot(3,i,k),'o','markersize',6,'markerfacecolor','r','markeredgecolor','k')
endif
hold on
endfor
%
% plotting Rosario
%
k=3;
for i=1:12
if (and(i>=1,i<3))
plot(Spot(1,i,k),Spot(3,i,k),'o','markersize',6,'markerfacecolor','g','markeredgecolor','k')
endif
if (i==3)
plot(Spot(1,i,k),Spot(3,i,k),'o','markersize',6,'markerfacecolor','y','markeredgecolor','k')
endif
hold on
endfor
%
% plotting CABA
%
k=4;
for i=1:12
if (or(i==12,i==1,i==2))
plot(Spot(1,i,k),Spot(3,i,k),'o','markersize',6,'markerfacecolor','g','markeredgecolor','k')
endif
if (i<12)
hold on
endif
endfor
%
% plotting query spots
%
% Asuncion
%
k=5;
for i=2:4
plot(Spot(1,i,k),Spot(3,i,k),'o','markersize',6,'markerfacecolor','k','markeredgecolor','k')
text(Spot(1,i,k),Spot(3,i,k)+0.5, strcat(char(names{k}),", ",months(i,:)),'fontsize',15)
endfor
%
% Corrientes
%
k=6;
for i=2:4
plot(Spot(1,i,k),Spot(3,i,k),'o','markersize',6,'markerfacecolor','k','markeredgecolor','k')
text(Spot(1,i,k),Spot(3,i,k)+0.5, strcat(char(names{k}),", ",months(i,:)),'fontsize',15)
endfor
%
% Santa Maria
%
k=7;
for i=3:5
plot(Spot(1,i,k),Spot(3,i,k),'o','markersize',6,'markerfacecolor','k','markeredgecolor','k')
text(Spot(1,i,k),Spot(3,i,k)+0.5, strcat(char(names{k}),", ",months(i,:)),'fontsize',15)
endfor
%
plot([R(1),R(2)],[Temp_R(1),Temp_R(2)],"--k","linewidth",1)
%
grid on
grid minor on
xlabel("Mean daily incident solar radiation (kWh/m^{2})",'fontsize',15);
ylabel("Mean air temperature (°C)",'fontsize',15);
axis([R(1),R(2),15,max_measure(3)])
%
%-------------------------------------------------------------------------------
figure 3 % mean temp and cloudiness
%-------------------------------------------------------------------------------
%
% plotting Rome
%
k=1;
for i=1:12
if (and(i>=6,i<9))
plot(Spot(2,i,k),Spot(3,i,k),'o','markersize',6,'markerfacecolor','g','markeredgecolor','k')
endif
if (or(i<6,i>9))
plot(Spot(2,i,k),Spot(3,i,k),'o','markersize',6,'markerfacecolor','r','markeredgecolor','k')
endif
if (i==9)
plot(Spot(2,i,k),Spot(3,i,k),'o','markersize',6,'markerfacecolor','y','markeredgecolor','g')
endif
hold on
endfor
%
% plotting Arona
%
k=2;
for i=1:12
if (i==5)
plot(Spot(2,i,k),Spot(3,i,k),'o','markersize',6,'markerfacecolor','g','markeredgecolor','k')
endif
if (and(i>=1,i<5))
plot(Spot(2,i,k),Spot(3,i,k),'o','markersize',6,'markerfacecolor','r','markeredgecolor','k')
endif
hold on
endfor
%
% plotting Rosario
%
k=3;
for i=1:12
if (and(i>=1,i<3))
plot(Spot(2,i,k),Spot(3,i,k),'o','markersize',6,'markerfacecolor','g','markeredgecolor','k')
endif
if (i==3)
plot(Spot(2,i,k),Spot(3,i,k),'o','markersize',6,'markerfacecolor','y','markeredgecolor','k')
endif
hold on
endfor
%
% plotting CABA
%
k=4;
for i=1:12
if (or(i==12,i==1,i==2))
plot(Spot(2,i,k),Spot(3,i,k),'o','markersize',6,'markerfacecolor','g','markeredgecolor','k')
endif
if (i<12)
hold on
endif
endfor
%
% plotting query spots
%
% Buenos Aires
%
i=2;
k=4;
plot(Spot(2,i,k),Spot(3,i,k),'o','markersize',6,'markerfacecolor','k','markeredgecolor','k')
text(Spot(2,i,k),Spot(3,i,k)-0.5, strcat(char(names{k}),", ",months(i,:)),'fontsize',15)
%
% Asuncion
%
k=5;
for i=2:4
plot(Spot(2,i,k),Spot(3,i,k),'o','markersize',6,'markerfacecolor','k','markeredgecolor','k')
text(Spot(2,i,k),Spot(3,i,k)+0.5, strcat(char(names{k}),", ",months(i,:)),'fontsize',15)
endfor
%
% Corrientes
%
k=6;
for i=2:4
plot(Spot(2,i,k),Spot(3,i,k),'o','markersize',6,'markerfacecolor','k','markeredgecolor','k')
text(Spot(2,i,k),Spot(3,i,k)-0.5, strcat(char(names{k}),", ",months(i,:)),'fontsize',15)
endfor
%
% Santa Maria
%
k=7;
for i=3:5
plot(Spot(2,i,k),Spot(3,i,k),'o','markersize',6,'markerfacecolor','k','markeredgecolor','k')
text(Spot(2,i,k),Spot(3,i,k)+0.5, strcat(char(names{k}),", ",months(i,:)),'fontsize',15)
endfor
%
plot([Cl(1),Cl(2)],[Temp_Cl(1),Temp_Cl(2)],"--k","linewidth",1)
%
grid on
grid minor on
xlabel("Fraction of the day mainly cloudy (%)",'fontsize',15);
ylabel("Mean air temperature (°C)",'fontsize',15);
axis([Cl(1),Cl(2),15,max_measure(3)])
%
%-------------------------------------------------------------------------------
% Plotting the scoring for each city according to the best model
%-------------------------------------------------------------------------------
%
switch best
case 1
%
% Scoring for the query spots according to model h
%
h=1;
for i=1:12
for k=1:length(names)
score(i,k) = x{h}(1)+x{h}(2)*Spot(1,i,k)+x{h}(3)*Spot(3,i,k);
endfor
endfor
%
figure(5) % Plotting of the Scoring for the query spots
%
for k=1:length(names)
plot([1:1:12],score(:,k),char(types{k}),"linewidth",1.5)
hold on
endfor
plot([1,12],[5,5],"--g","linewidth",1.5)
title(model{h},'fontsize',15)
legend(char(names{1:length(names)}),"location","southwest",'fontsize',15)
xlabel("Month",'fontsize',15);
ylabel("Score",'fontsize',15);
grid on
grid minor on
case 2
%
% Scoring for the query spots according to model h
%
h=2;
for i=1:12
for k=1:length(names)
score(i,k) = x{h}(1)+x{h}(2)*Spot(2,i,k)+x{h}(3)*Spot(3,i,k);
endfor
endfor
%
figure(5) % Plotting of the Scoring for the query spots
%
for k=1:length(names)
plot([1:1:12],score(:,k),char(types{k}),"linewidth",1.5)
hold on
endfor
plot([1,12],[5,5],"--g","linewidth",1.5)
title(model{h},'fontsize',15)
legend(char(names{1:length(names)}),"location","southwest",'fontsize',15)
xlabel("Month",'fontsize',15);
ylabel("Score",'fontsize',15);
grid on
grid minor on
case 3
%
% Scoring for the query spots according to model h
%
h=3;
for i=1:12
for k=1:length(names)
score(i,k) = x{h}(1)+x{h}(2)*Spot(1,i,k)+x{h}(3)*Spot(2,i,k)+x{h}(4)*Spot(3,i,k);
endfor
endfor
%
figure(5) % Plotting of the Scoring for the query spots
%
for k=1:length(names)
plot([1:1:12],score(:,k),char(types{k}),"linewidth",1.5)
hold on
endfor
plot([1,12],[5,5],"--g","linewidth",1.5)
title(model{h},'fontsize',15)
legend(char(names{1:length(names)}),"location","southwest",'fontsize',15)
xlabel("Month",'fontsize',15);
ylabel("Score",'fontsize',15);
grid on
grid minor on
case 4
%
% Scoring for the query spots according to model h
%
h=4;
for i=1:12
for k=1:length(names)
score(i,k) = x{h}(1)+x{h}(2)*Spot(1,i,k)+x{h}(3)*(Spot(3,i,k)^4);
endfor
endfor
%
figure(5) % Plotting of the Scoring for the query spots
%
for k=1:length(names)
plot([1:1:12],score(:,k),char(types{k}),"linewidth",1.5)
hold on
endfor
plot([1,12],[5,5],"--g","linewidth",1.5)
title(model{h},'fontsize',15)
legend(char(names{1:length(names)}),"location","southwest",'fontsize',15)
xlabel("Month",'fontsize',15);
ylabel("Score",'fontsize',15);
grid on
grid minor on
case 5
%
% Scoring for the query spots according to model h
%
h=5;
for i=1:12
for k=1:length(names)
score(i,k) = x{h}(1)+x{h}(2)*Spot(1,i,k)+x{h}(3)*Spot(3,i,k)+x{h}(4)*(Spot(3,i,k)^4);
endfor
endfor
%
figure(5) % Plotting of the Scoring for the query spots
%
for k=1:length(names)
plot([1:1:12],score(:,k),char(types{k}),"linewidth",1.5)
hold on
endfor
plot([1,12],[5,5],"--g","linewidth",1.5)
title(model{h},'fontsize',15)
legend(char(names{1:length(names)}),"location","southwest",'fontsize',15)
xlabel("Month",'fontsize',15);
ylabel("Score",'fontsize',15);
grid on
grid minor on
case 6
%
% Scoring for the query spots according to model h
%
h=6;
for i=1:12
for k=1:length(names)
score(i,k) = x{h}(1)+x{h}(2)*((273.15+Spot(3,i,k))^4);
endfor
endfor
%
Plot_score (score, h, model, names, types, spline)
case 7
%
% Scoring for the query spots according to model h
%
h=7;
for i=1:12
for k=1:length(names)
score(i,k) = x{h}(1)+x{h}(2)*Spot(3,i,k)+x{h}(3)*((273.15+Spot(3,i,k))^4);
endfor
endfor
%
Plot_score (score, h, model, names, types, spline)
endswitch
%
%-------------------------------------------------------------------------------
% We save the data for the regressions
%-------------------------------------------------------------------------------
%
save("M.csv","M")
save("Y.csv","b")